
Here are short summaries of the projects I was a part of during my Ph.D. Expect a mix of algebraic topology, graph theory, and evolutionary biology.
It’s all about how DNA is scrambled
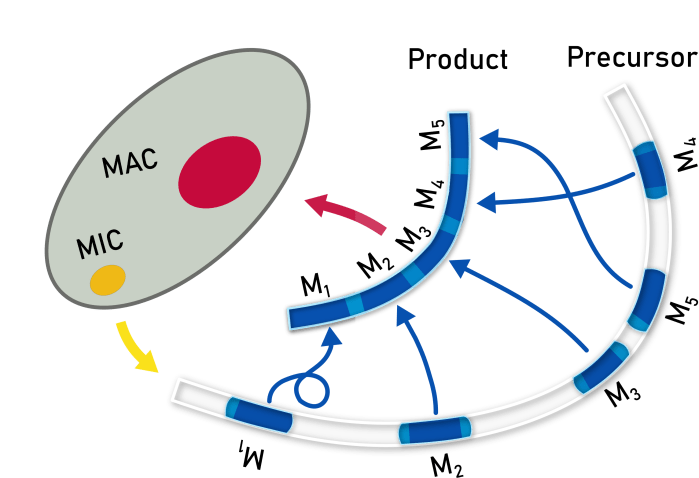
Oxytricha trifallax is a model organism for genome rearrangement. Each cell contains two types of nuclei: macronoclei (MAC) where DNA is ready to be transcribed and micronuclei (MIC) where the same information is stored but each gene (*ahem*, contig) has been separated into segments that may appear out of order or in reversed orientation. During reproduction, the MAC is destroyed and regenerated from the MIC. The work here models DNA strands in the MIC by labeling the ends of segments that will join together (pointers). These can be identified in as short repeat sequences that appear twice in the MIC, of which only one copy is retained in the MAC.
Prodsimplicial cell complexes on directed graphs
One way to model the recombination process is through deletions of patterns in words on the alphabet of pointer labels. If we use these words as vertices and connect them when a pattern deletion leads from one to the other, the level of scrambling can be quantified through homology groups on a complex built on the graph.
Prodsimplicial cells are defined through the Cartesian product of directed simplices, and I study the homology groups for families of graphs using this as the foundation for a new cell complex. In this complex, parallel paths of length two are identified, as well as two step reductions parallel to single step reductions. The holes that remain after endowing the graph wireframe with the prodsimplicial cells correspond to different reduction pathways: the more pathways are possible between one word and the empty word, the more scrambled the segments that word models is.
You can learn more about this project on its GitHub repository.
Counting gene segment arrangements
A single DNA strand may encode different genes, so the model above is in fact a simplified one. It is of interest whether some multiple-gene arrangements are more prevalent than others. Samples of observed arrangements can be compared to those that are theoretically possible. As a generalization of DOWs, reduction rules and rearrangement complexity measures can also be defined to determine whether properties of legal strings are suitable invariants to analyze genomes.
Cryptic pointers and DNA circularization
It has been experimentally observed that during recombination, portions of Oxytricha trifallax’s genome are excised as circular molecules by Yerlici et al (“Programmed genome rearrangements in Oxytricha produce transcriptionally active extrachromosomal circular DNA,” 2019). Since pointers guide the process of joining gene segments, the DNA sequences in a neighborhood of the circles’ start and end position were examined for repeat sequences (cryptic pointers). With the help of python scripts, the longest common substrings within some window of the endpoints were obtained under varying conditions simulating different models for cyclization and allowed errors in the repeats.

